1 Introduction

Power losses in distribution systems may be significant and may negatively affect the economics of electric power distribution networks [1]. Consequently, it is of interest to study the reduction of losses through techniques such as distribution network reconfiguration (DNR). The topology of power distribution systems is typically radial, whereas transmission systems can operate in loop or radial configurations [2].

Radial distribution systems often feature sectionalizing switches and tie switches, mainly used for fault isolation, power supply recovery and system reconfiguration.

These switches allow for reconfiguring the topology of the network, with the objectives being reduction of power losses, load balancing, and improvement of voltage profile and system reliability [3]. A large number of permutations, resulting from all possible switch configurations, make the network reconfiguration task a complex and non-linear combinatorial problem, particularly for large systems. Due to the power flow calculations involved [4], the incurred computational cost can be considerable.

The first example of DNR for power loss reduction [5] was a branch and bound search with all tie lines initially closed, thus creating a meshed system; subsequently switch opening was done until a radial configuration was achieved. Similarly, a method was proposed in [6], where the network was initially meshed and the switches were ranked based on the current carried. The top-ranked switch was opened and the power flow calculation was carried out. The process was repeated until the system was radial. A branch exchange was performed wherever a loop had been identified. The configuration with lower power losses was kept.

In [7], a generalized approach was proposed in which the tie line with the highest voltage difference was closed and the neighbouring branch was opened in the loop formed, leading to a reduction of power losses. Reference [8] implemented DNR through node-depth encoding (NDE), which improved the performance of evolutionary algorithms and power flow algorithms. On average, 27.64% in loss reduction was obtained on 30880 buses in a 5166-switch system.

The DNR problem is, in general, a multi-modal one, and hence computational intelligence algorithms are normally more appropriate, even though they generally do not converge to the global optima for larger size systems.

In [2], DNR was performed using the cuckoo search algorithm (CSA) on 33-, 69- and 119-node distribution systems and compared to methods presented in other works. The power loss values presented for the 33- and 69-node systems were the same as those implementing continuous genetic algorithm (CGA) and particle swarm optimization (PSO); the losses were smaller than those applying fireworks algorithm (FWA) [9], genetic algorithm (GA), refined GA (RGA), improved tabu search (ITS), harmony search algorithm (HSA) [10], ant colony (AC) algorithm, and improved adaptive imperialist competitive algorithm (IAICA) [11]. For the 119-node system, CSA and CGA presented the same loss level, where FWA and HSA presented the lowest.

For larger distribution systems (with hundreds or thousands of buses), DNR can be computationally expensive and requires unacceptable computing time.

Power flow analysis is an essential task of DNR, necessary to evaluate the status of the distribution network before and after reconfiguration. Thus, it serves as a reference to determine the effects of network reconfiguration on quantities of interest (e.g., line power losses and/or voltage profile). Due to the multi-combinatorial nature of DNR, a large number of power flow analyses are required [12].

The usual radial topology of distribution networks has driven power flow analysis to be done with techniques such as the forward-backward sweep ladder method [13], because traditional methods such as the decoupled version of Newton Raphson have shown convergence problems leading to undesirable solutions [14].

The Open Distribution System Simulation (OpenDSS) is an efficient and fast simulation tool for distribution network analysis. It can perform power flow analysis although it evolved as a harmonic flow analysis tool [15]. It handles not only radial networks but arbitrarily-meshed, multi-phase networks. The power flow solving methods implemented by OpenDSS are based on the “current injection mode”. The use of the Newton method enables OpenDSS to be a fast and robust power flow analysis tool [16].

In this paper, a customized evolutionary algorithm has been proposed for solving a DNR problem for radial networks. The major differences between conventional evolutionary algorithms and the proposed one are in dedicated recombination operators that embed specific knowledge of the problem. By enforcing feasibility of solutions, particularly maintaining radial network structure at all stages of the process, a considerable reduction of the search space size is obtained. This leads to faster convergence of the optimization process, as well as improved repeatability of the results, based on the numerical studies carried out for the 33-, 69-, and 119-bus test problems. More importantly, comprehensive benchmarking indicates superiority of the proposed technique over state-of-the-art algorithms reported in the literature.

2 Problem formulation

2.1 Objective function

Network reconfiguration is realized by changing the state of the switches (open/close). The objectives of this change in the system are to minimize the power losses and to improve the voltage profile/index. In more rigorous terms, the objective is to minimize the expression in (1) [9]:

$$F = \Delta P_{\text{loss}}^{\text{ratio}} + \Delta V_{\text{D}}$$
(1)

where \(\Delta P_{\text{loss}}^{\text{ratio}}\) is the ratio of the total power loss in the branches after reconfiguration \(\Delta P_{\text{loss}}^{\text{rec}}\) to the initial power losses before reconfiguration \(\Delta P_{\text{loss}}^{\text{init}}\), as in (2); ΔVD is the voltage variation index and calculated by finding the maximum voltage drop for all buses using the ratios of bus voltages Vi to the reference source voltage V1, as in (3):

$$\Delta P_{\text{loss}}^{\text{ratio}} = P_{\text{loss}}^{\text{rec}} /P_{\text{loss}}^{\text{init}}$$
(2)
$$\Delta V_{\text{D}} = \mathop {\hbox{max} }\limits_{{i = 1,2, \cdots ,N_{\text{bus}} }} \left| {1 - V_{i} /V_{1} } \right|$$
(3)

In (1), one takes into account the change in losses after the reconfiguration as well as the deviation of voltage in relation to the base voltage, and aims to minimize both parameters. The constraint is to maintain the radial architecture of the network, for supplying all load points.

The network power losses are calculated by adding up the losses in all active network branches, as in (4), where Pi and Qi represent the active and reactive power flow out of bus i, respectively; Ri is the resistance of line segment i; Vi is the voltage at the ith bus; Nbr is the number of active branches, given by (5):

$$P_{\text{loss}} = \sum\limits_{i = 1}^{{N_{\text{br}} }} {R_{i} \frac{{P_{i}^{2} + Q_{i}^{2} }}{{V_{i}^{2} }}}$$
(4)
$$N_{\text{br}} = N_{\text{bus}} - 1$$
(5)

2.2 Power flow

OpenDSS is utilized to carry out power flow simulations of the test distribution systems described in Section 4. For the radial circuits, as the considered ones here, OpenDSS exhibits convergence characteristics similar to those of forward-backward sweep methods [15].

The test distribution systems are modeled as power delivery elements (power lines) and power conversion elements (loads) in the OpenDSS environment. The OpenDSS script-driven simulation engine has a component object model (COM) which allows MATLAB command to access OpenDSS features as illustrated in Fig. 1. Some of the commands include switch operations, power flow execution, results extraction, etc.

Fig. 1
figure 1

Main simulation engine of OpenDSS accessible to MATLAB command

Full size image

Switching operations require a switch control assigned to every branch in the network; given sectionalizing switches Nsec and tie switches Nts, the total number of controlled switches Ns is given by (6):

$$N_{\text{s}} = N_{ \sec } + N_{\text{ts}}$$
(6)

The switches status is expressed by a binary string x with zeros representing open switches and ones representing closed switches.

3 Optimization methodology

In this section, the proposed optimization algorithm is outlined. It is referred to as feasibility-preserving evolutionary optimization (FPEO). Similar to the previous works in the literature, as in [2], a population-based metaheuristic method is selected due to its ability to perform global search. This is necessary because DNR is intrinsically a multi-modal problem. The algorithm is tailored to the task at hand, in particular, a radial network configuration is maintained throughout the optimization run. The operation and performance of the method is demonstrated in Section 4.

3.1 Representation

The solutions are represented as binary strings with zeros corresponding to open switches (no connection) and ones corresponding to close switches (existing connections).

Given Nbr and Nts, the number of possible network configurations is C(Nbr, Nts) which is large and grows quickly with both Nbr and Nts. At the same time, the number of radial configurations, equal to the number of the spanning trees τ(G) of the network graph G, is much smaller. For example, for the 119-bus system in [17], the numbers are 2.4×1019 and 4×1015 (the latter estimated using the matrix-tree theorem [18]). Consequently, it is beneficial to maintain feasibility of solutions throughout the entire optimization run. In the proposed algorithm, it is realized by appropriate definition of the recombination and mutation operators.

3.2 Algorithm flow

The proposed algorithm follows the basic steps of the generational evolutionary algorithms. The flow diagram of the proposed algorithm is shown in Fig. 2, where P stands for the population.

Fig. 2
figure 2

Flow diagram of proposed algorithm

Full size image

The algorithm uses binary tournament selection [19]. It also features elitism and adaptive adjustment of mutation probability based on population diversity. The elitism works by replacing the first individual of the newly created population by the best individual found so far, which allows it to bypass the selection and recombination procedures, and, thereby, to preserve it across the algorithm iterations. Diversity is measured as the average standard deviation of solution components. The vector F of cost function values for the population is used by the selection procedure. The two critical (and novel) components of the algorithm are mutation and crossover operators, both designed to maintain radial structure of the network. They are briefly described in the following two subsections.

3.3 Feasibility-preserving mutation operator

The mutation operator is supposed to introduce a small random change in the network configuration. Here, it is implemented as follows. First, one of the open switches is randomly selected and closed creating a loop in the network. Then, the loop created this way is identified. Finally, one of the connections on the loop is randomly selected to be opened. As a result, the network is transformed from one radial configuration to another. The mutation operator has also been explained in Fig. 3.

Fig. 3
figure 3

Operation of feasibility-preserving mutation operator

Full size image

3.4 Feasibility-preserving crossover operator

The crossover operator, similarly as the mutation one, is designed to maintain radial configuration of the network. The first step is a conventional uniform crossover [20], where components of the offspring x are randomly selected from one of the two parent individuals. In the second step, a repair procedure is launched according to the flow diagram shown in Fig. 4, where G(x) represents the network graph corresponding to the configuration x.

Fig. 4
figure 4

Flow diagram of repair procedure

Full size image

In the above algorithm, connectivity of the network graph is first checked. In case the graph is not connected, subsequent switches are closed until connectivity is achieved. At this step, only those switches that do not lead to creating loops can be closed. Otherwise, subsequent connections are opened until the network graph becomes a tree which corresponds to a radial network configuration. While modifying the individual, the switches that have already been tried out are stored in order to avoid unnecessary repetitions. The flow diagram of the crossover operator is shown in Fig. 5.

Fig. 5
figure 5

Flow diagram of feasibility-preserving crossover operator

Full size image

It should be emphasized that due to the repair procedure, the network modification made by a crossover operation can be quite extensive, especially in the initial stages of the optimization run when diversity of the population is large. Consequently, a low crossover probability is used (here, 0.2), which is more advantageous as indicated by the initial experiments.

4 Numerical results and benchmarking

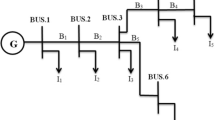
In this section, the FPEO algorithm introduced in Section 3 has been comprehensively validated using 3 standard test networks [16, 17, 21], consisting of 33, 69 and 119 buses, presented in Figs. 6, 7 and 8, respectively. The network topologies are briefly discussed in Section 4.1. Numerical results are presented in Section 4.2 along with comparison to state-of-the-art methods from the literature.

Fig. 6
figure 6

33-bus distribution system

Full size image
Fig. 7
figure 7

69-bus distribution system

Full size image
Fig. 8
figure 8

119-bus distribution system

Full size image

4.1 Test cases

The systems are assumed to be balanced and hence single phase representation is sufficient.

The initial conditions of the systems, obtained from the power flow method outlined in Section 2.2, are described in Table 1, where Vmin is the minimum voltage found in the system, for all busses, and the “Initial loss” is the total system power losses. For power flow purposes, the L-N base voltage level for the 33- and 69-bus systems is set to be 12.66 kV, while for the 119-bus system, the base voltage level set is 11 kV; a tolerance threshold of 0.005 is set.

Table 1 Initial parameters of test distribution networks
Full size table

The initial topologies of the considered systems are shown in Figs. 6, 7 and 8. Each bus is indexed for easy identification. The discontinuous lines represent the tie lines, and each is labeled with the switch number of the switch that operates the tie line.

Based on the fact that the voltage source operates as a Thevenin equivalent source, the complex impedance, set during the modelling in the OpenDSS environment, is the impedance of the first line connected to the voltage source bus.

4.2 Results and benchmarking

The proposed algorithm has been executed using the following setup: population size 10, crossover probability 0.2, and mutation probability 0.2. It should be noted that these values are different from typical ones utilized in evolutionary algorithms (e.g., 0.5 to 0.9 for crossover, and 0.01 to 0.05 for mutation). Extensive initial experiments conducted for various values of the control parameters (e.g., crossover rate between 0.1 and 0.5, mutation rate between 0.05 and 0.2) indicate that the values utilized above provide the best results, however, the algorithm works relatively well also for other setups within the aforementioned ranges. In particular, the cost function averaged over 20 independent runs may increase up to a few percent as compared to the algorithm using the control parameter values.

As already explained in Section 3.4, the dedicated crossover operator designed for FPEO is rather disruptive so that lower crossover probability has to be used. Suitable values of this and other parameters such as population size and mutation probability have been obtained through initial experiments. In particular, higher mutation probability is necessary in order to maintain sufficient population diversity (although a particular value of 0.2 is not critical because it is adaptively adjusted during the optimization run).

Maximum number of function evaluations was set to 500, 1000, and 5000 for 33-, 69- and 119-bus systems, respectively, which corresponds to 50, 100, and 500 algorithm iterations. The results are shown in Tables 2, 3 and 4, for 33-, 69- and 119-bus systems, respectively. In Tables 2, 3 and 4, different power losses for the same network configuration in some instances are due to different simulation software packages used by various authors; Nevals is the number of cost function evaluations, equal to the population size times number iterations; N/A means that relevant data has not been provided.

Table 2 Statistics of the optimization results of the 33-bus test network
Full size table
Table 3 Statistics of the optimization results of the 69-bus test network
Full size table
Table 4 Statistics of the optimization results of the 119-bus test network
Full size table

FPEO has been executed 20 times in order to obtain meaningful statistical data. The results obtained for the 33-bus test network are compared to those presented in [2, 9, 10]; configurations presented by the specified references are simulated using the power flow method described in Section 2.2.

As shown in Table 2, the power losses are slightly higher than those presented in [2], RGA in [15] and GA in [10], however, the fitness function value of the proposed method exhibits the lowest value. The reason is objective aggregation, as indicated in (1), i.e. the objective function value is a composition of the power losses and the bus voltage index.

It should be emphasized that repeatability of the results is excellent for the proposed FPEO: e.g. in this case the algorithm returns the globally optimum results in all runs (i.e., zero standard deviation). This is not the case for the benchmark methods as shown in Table 2. Thus, the reliability of FPEO significantly exceeds reliability of other techniques.

For the 69-bus test network, the results are consistent with those obtained for the 33-bus network, i.e., globally optimum results have been obtained in all algorithm runs as shown in Table 3. For the 119-bus test network, the results are presented in Table 4. The configuration obtained is the same as that of CSA in [2], FWA in [9] and CGA in [2]. The results for PSO [2] and modified tabu search (MTS) [22] are also presented. As indicated in Table 4, the statistical data reflects a clear indication that FPEO obtains global optima for vast majority of runs (19 out 29; the standard deviation is very low).

Figures 9, 10 and 11 show the optimization history for the 3 considered test cases. In Figs. 9, 10 and 11, red lines indicate objective function value versus iteration index for 20 algorithm runs; the black line is an average value. The optimum value is obtained for all but one algorithm runs with the algorithm being virtually converged after 35–40 iterations (which corresponds to 350–400 system simulations) for Fig. 9 (cf. Table 2), and after 50–60 iterations (which corresponds to 500–600 system simulations) for Fig. 10 (cf. Table 3). The optimum value has been obtained for most of the algorithm runs for Fig. 11 (cf. Table 4).

Fig. 9
figure 9

Optimization history for 33-bus system

Full size image
Fig. 10
figure 10

Optimization history for 69-bus system

Full size image
Fig. 11
figure 11

Optimization history for 119-bus system

Full size image

It can be observed that the evolution of the objective function (versus iteration index) is consistent for all algorithm runs thus confirming its robustness. The voltage profiles and power losses before (initial) and after the optimization (optimized) are shown in Figs. 12 and 13, respectively, which confirm the voltage profile improvement. After the optimized reconfiguration, the minimum p.u. voltage is increased to 0.9383, 0.9430 and 0.9305 p.u. for 33-, 69- and 119-bus networks respectively.

Fig. 12
figure 12

Network voltage profile before and after reconfiguration/optimization

Full size image
Fig. 13
figure 13

Network power losses before and after reconfiguration/ optimization

Full size image

4.3 Discussion

FPEO has been demonstrated to be a viable method for solving power distribution system reconfiguration based on the radial nature of the distribution systems. The globally optimum configurations have been found for all considered test cases.

The improvement in power losses is significant and although the voltage profile was not directly controlled (cf. (1)), the optimized configurations exhibit significant improvement with this respect.

OpenDSS is used in this work to solve power flow, and although power flow method is different than that utilized by the benchmark methods, the numerical results are very close.

There are two features of FPEO that have to be emphasized. The first one is robustness. As opposed to majority of benchmark approaches, FPEO features excellent repeatability of results (globally optimum solutions obtained in all algorithm runs for 33- and 69-bus systems and all but one for 119-bus network). Second, the computational cost of the algorithm is dramatically lower than that of majority of the benchmark approaches. For example, the CSA, CGA, and PSO methods in [2] are set to 3000 function evaluations for 33- and 69-bus system, and 15000 evaluations for 119-bus system. FPEO works with 500, 1000 and 5000 maximum function evaluations for the 3 systems, respectively. In other words, FPEO offers a much faster convergence rate.

5 Conclusion

In the paper, a customized evolutionary algorithm for solving distribution network reconfiguration problem has been presented. The proposed algorithm determines the optimized configuration of the network with respect to objectives being reduction of the power losses and improvement of the voltage profile.

The proposed algorithm features feasibility preserving mutation and recombination operators which allow us to maintain the radial structure of the network at all steps of the optimization process, which results in a dramatic reduction of the search space size.

As demonstrated, through comprehensive numerical validation, the proposed technique is superior over majority of the state-of-the-art methods reported in the literature. In particular, the computational cost of the optimization process is much lower than for most of competitive approaches. More importantly, repeatability of results is excellent, allowing for obtaining a globally optimum solution in almost each and every algorithm run.

The future work will be focused on extending the range of applications of the method, including multi-objective DNR (for both power loss reduction and voltage control), constrained optimization, as well as other types of networks (multi-source, non-radial).