1 Introduction

With expected long term rising fossil fuel prices and declining prices of photovoltaic (PV) cells and modules, PV power systems continue to grow around the world and become one of the least cost options of renewable electricity [1]. With high penetration of PV systems into the grid, the impact of PV systems on the grid becomes more and more significant [2]. One of the most important issues is the power quality from grid-connected inverters [3–5]. The grid-connected inverter may inject harmonics and thus pollute the grid. IEEE Std. 929-2000 specified that the total harmonic distortion of the injected grid current must be less than 5% [6]. Therefore, it is important to regulate the grid-connected inverter to achieve the sinusoidal current injection.

Many interesting control proposals have been reported in the past decades. A method to improve the inverter output current by using the capacitor current feedforward disturbance rejection was proposed in [7]. Reference [8] presented a method via the grid feed forward and the multi-harmonic resonant control for the current quality improvement. Another interesting method in [9] achieved the harmonic cancellation for grid-connected inverters by randomizing a tuning parameter of the current controller. Note that the abovementioned methods are mainly for single-phase grid-connected inverters. For three-phase grid-connected inverters, further requirements should be considered. The grid current should follow the fundamental positive sequence component of the grid voltage with a preset current value. That’s why so many phase-locked loops have been proposed in recent years [10–17]. In [10], a method for extracting the fundamental frequency positive-sequence voltage was proposed based on the simple mathematical transformations. Another interesting method in [11] utilized the decoupled double synchronous reference frame phase-locked loop. An improvement in [12] used an adaptive synchronous reference frame phase-locked loop. A multiple reference frame based phase-locked loop was reported in [13] to extract the fundamental positive sequence component of the grid voltage. Also, multiple reference frame based PI control was used to maintain a balanced set of three-phase sinusoidal currents. However, the method required many reference frame transformations and increased the computational burden. Therefore, the phase-locked loop and control strategy without any frame transformations needs further investigation.

The objective of this paper is to present a new abc frame complex-coefficient filter and controller to improve the current quality of the three-phase grid-connected inverter. This paper is organized as follows. Section 2 presents the control strategy including the detailed implementation of the abc frame complex-coefficient filter and controller. The experimental verification of the proposed method is presented in Section 3. Finally, the conclusion is provided in Section 4.

2 Proposed control strategy

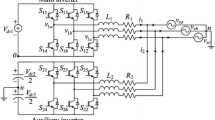
The schematic diagram of a three-phase grid-connected inverter is illustrated in Fig. 1, where an LCL filter is used to attenuate the high-frequency harmonics due to switching [18, 19]. The control objective is to inject sinusoidal currents into the grid, which complies with the relevant IEEE Standard [6].

Fig. 1
figure 1

Schematic diagram of three-phase grid-connected inverter

Full size image

In practice, the grid voltage is polluted with harmonics, which can be mathematically expressed as (1), where \(U_{M}^{ + }\) and \(\omega_{0}\) are the amplitude and angular frequency of fundamental positive sequence component of three-phase grid voltage respectively; n is the harmonic order; \(U_{N}\) and \(\varphi_{N}\) are the amplitude and phase of harmonic component of grid voltage respectively.

$$\begin{aligned}& \left[ {\begin{array}{c} {U_{a} } \\ {U_{b} } \\ {U_{c} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {U_{a}^{ + } } \\ {U_{b}^{ + } } \\ {U_{c}^{ + } } \\ \end{array} } \right] + \left[ {\begin{array}{c} {\sum U_{a}^{h} } \\ {\sum U_{b}^{h} } \\ {\sum U_{c}^{h} } \\ \end{array} } \right] = \hfill \\ & \qquad \qquad \left[ {\begin{array}{*{20}c} {U_{M}^{ + } \sin (\omega_{0} t) + \sum U_{N} \sin (n\omega_{0} t + \varphi_{N} )} \\ {U_{M}^{ + } \sin (\omega_{0} t - 120^\circ ) + \sum U_{N} \sin (n\omega_{0} t - 120^\circ + \varphi_{N} )} \\ {U_{M}^{ + } in(\omega_{0} t + 120^\circ ) + \sum U_{N} \sin (n\omega_{0} t - 120^\circ + \varphi_{N} )} \\ \end{array} } \right] \hfill \\ \end{aligned}$$
(1)

In this case, the grid current should follow the fundamental positive sequence component of three-phase grid voltage. The current reference is defined as follows:

$$\left\{ \begin{aligned} I_{a}^{*} = \sqrt {\frac{3}{2}} \frac{{U_{a}^{ + } }}{{\sqrt {(U_{a}^{ + } )^{2} + (U_{b}^{ + } )^{2} \, + (U_{c}^{ + } )^{2} } }}I_{M}^{*} = \frac{{U_{a}^{ + } }}{{U_{M}^{ + } }}I_{M}^{*} \hfill \\ I_{b}^{*} = \sqrt {\frac{3}{2}} \frac{{U_{b}^{ + } }}{{\sqrt {(U_{a}^{ + } )^{2} + (U_{b}^{ + } )^{2} \, + (U_{c}^{ + } )^{2} } }}I_{M}^{*} = \frac{{U_{b}^{ + } }}{{U_{M}^{ + } }}I_{M}^{*} \hfill \\ I_{c}^{*} = \sqrt {\frac{3}{2}} \frac{{U_{c}^{ + } }}{{\sqrt {(U_{a}^{ + } )^{2} + (U_{b}^{ + } )^{2} \, + (U_{c}^{ + } )^{2} } }}I_{M}^{*} = \frac{{U_{c}^{ + } }}{{U_{M}^{ + } }}I_{M}^{*} \hfill \\ \end{aligned} \right.$$
(2)

From (2), it can be observed that the fundamental positive sequence component of grid voltage should be estimated for the current reference generation, which could be achieved by a new method proposed in Fig. 2. The basic idea of the proposed method is to eliminate the fundamental negative sequence component and attenuate the harmonic components of the grid voltage with the complex-coefficient filters. Different from the method in [20], the proposed method is simple and based on abc frame with no need of any frame transformation. In this way, the fast and accurate estimation of the fundamental positive sequence component can be achieved.

Fig. 2
figure 2

Proposed estimation method

Full size image

The following mathematical equations can be obtained from Fig. 2, where i = a, b, or c. \(\omega_{C}\) is the cutoff frequency, and \(\omega_{C} = 0.707\omega_{0}\) in this paper.

$$\hat{U}_{i}^{ + } (s) = \frac{{\omega_{C} }}{{s - j\omega_{0} + \omega_{C} }}[U_{i} (s) - \hat{U}_{i}^{ - } (s)]$$
(3)
$$\hat{U}_{i}^{ - } (s) = \frac{{\omega_{C} }}{{s + j\omega_{0} + \omega_{C} }}[U_{i} (s) - \hat{U}_{i}^{ + } (s)]$$
(4)

With (3) and (4), the transfer function of the estimated fundamental positive sequence component can be expressed as:

$$\hat{U}_{i}^{ + } (s) = \frac{{\omega_{C} (s + j\omega_{0} )}}{{s^{2} + 2\omega_{C} s + \omega_{0}^{2} }}U_{i} (s) = F(s)U_{i} (s)$$
(5)

where the magnitude of F(s) is:

$$\left| {F(s)} \right| = \frac{{\left| {\omega_{C} (\omega + \omega_{0} )} \right|}}{{\sqrt {(\omega_{0}^{2} - \omega^{2} )^{2} + (2\omega_{C} \omega )^{2} } }}$$
(6)

From (5) and (6), it can be concluded that the fundamental negative sequence component is eliminated and harmonic components are attenuated. While the fundamental positive sequence component of three-phase grid voltage remains unchanged without any attenuation or phase shift.

Fig. 3a shows the implementation of the proposed method. It should be noted that the complex coefficient j can be smartly implemented in abc frame. And the corresponding method is shown in Fig. 3b.

Fig. 3
figure 3

Detailed implementation of the proposed method

Full size image

In summary, the fundamental-frequency positive sequence component of three-phase grid voltage can be obtained with the proposed method in Fig. 3b. And then the current reference can be easily obtained from (2).

In order to ensure that the grid current tracks the current reference, a closed-loop control strategy is generally used. The single-line diagram of the control structure for three-phase grid-connected inverter is shown in Fig. 4, where C(s) is the current controller, K is the pulse width modulation (PWM) gain, R 2 is the resistor used for the passive damping [19], and U g is the grid voltage.

Fig. 4
figure 4

Single-line diagram of the control structure

Full size image

The grid current can be derived from Fig. 4 as:

$$\begin{aligned} &I_{2} (s) = R(s)I_{2}^{*} (s) - \frac{{U_{g} (s)}}{Y(s)} = \\ &\qquad \quad \frac{KC(s)N(s)}{1 + KC(s)N(s)}I_{2}^{*} (s) - \frac{{U_{g} (s)}}{{\frac{1}{H(s)N(s)} + \frac{KC(s)}{H(s)}}} \\ \end{aligned}$$
(7)

where \(N(s) = \frac{{(L_{2} s + R_{2} )}}{{L_{1} L_{2} R_{2} Cs^{3} + L_{1} L_{2} s^{2} + R_{2} (L_{1} + L_{2} )s}}\); \(H(s) = L_{1} Cs^{2} + 1\).

The control objective is that the grid current tracks the current reference, which means R(s) = 1 and \(Y(s) = \infty\). From the viewpoint of superposition theorem, \(I_{2} (s) = I_{2}^{*} (s)\).

To achieve the abovementioned control objective, a new abc-frame complex coefficient controller is proposed as shown in (8) and Fig. 5, where \(\omega_{x}\)is the angular frequency, and can be adjusted according to the specified requirements.

$$C(s) = \frac{N(s)}{{(s - j\omega_{x} )D(s)}}$$
(8)
Fig. 5
figure 5

Implementation of the proposed complex-coefficient controller

Full size image

Substituting (8) into (7), it can be concluded that R(s) = 1 and \(Y(s) = \infty\) when \(\omega_{x}\) matches the frequency of the current reference or grid voltage. In this way, both the perfect tracking of the current reference and disturbance rejection of grid voltage harmonic can be achieved. It should be noted that the harmonic amplitude of the grid voltage tends to be lower as the harmonic order increases. Therefore, only the low-order harmonics are considered, e.g., \(\omega_{x} = \omega_{0} , - \omega_{0} , - \omega_{5} ,\omega_{7}\).

To further simplify the controller, assume D(s) = 1 and N(s) = k x . Also a proportional term can be integrated into the controller. The above-mentioned complex-coefficient filters and controller are implemented with the third order integrator in a discrete-time form [20].

$$\frac{y(s)}{u(s)} = \frac{1}{s} \, \Leftrightarrow \, \frac{y(z)}{u(z)} = \frac{{T_{s} }}{12}\frac{{23z^{ - 1} - 16z^{ - 2} + 5z^{ - 3} }}{{1 - z^{ - 1} }}$$
(9)
$$y(n) = y(n - 1) + \frac{{T_{s} }}{12}[23u(n - 1) - 16u(n - 2) + 5u(n - 3)]$$
(10)

where \(u\) and \(y\) are the input and output of integrator respectively; and \(T_{s}\) is the sample period.

The digital forms of the filters and controllers are presented as:

$$\left\{ \begin{aligned} &u_{a}^{ + } (n - 1) = \frac{{\omega_{C} [U_{a} (n - 1) - \hat{U}_{a}^{ + } (n - 1) - \hat{U}_{a}^{ - } (n - 1)] - \omega_{0} [\hat{U}_{a}^{ + } (n - 1) + 2\hat{U}_{b}^{ + } (n - 1)]}}{\sqrt 3 } \\ &\hat{U}_{a}^{ + } (n) = \hat{U}_{a}^{ + } (n - 1) + \frac{{T_{s} }}{12}[23u_{a}^{ + } (n - 1) - 16u_{a}^{ + } (n - 2) + 5u_{a}^{ + } (n - 3)] \\ & u_{a}^{ - } (n - 1) = \frac{{\omega_{C} [U_{a} (n - 1) - \hat{U}_{a}^{ + } (n - 1) - \hat{U}_{a}^{ - } (n - 1)] + \omega_{0} [\hat{U}_{a}^{ - } (n - 1) + 2\hat{U}_{b}^{ - } (n - 1)]}}{\sqrt 3 } \\ &\hat{U}_{a}^{ - } (n) = \hat{U}_{a}^{ - } (n - 1) + \frac{{T_{s} }}{12}[23u_{a}^{ - } (n - 1) - 16u_{a}^{ - } (n - 2) + 5u_{a}^{ - } (n - 3)] \\ & u_{b}^{ + } (n - 1) = \frac{{\omega_{C} [U_{b} (n - 1) - \hat{U}_{b}^{ + } (n - 1) - \hat{U}_{b}^{ - } (n - 1)] + \omega_{0} [\hat{U}_{b}^{ + } (n - 1) + 2\hat{U}_{a}^{ + } (n - 1)]}}{\sqrt 3 } \\ &\hat{U}_{b}^{ + } (n) = \hat{U}_{b}^{ + } (n - 1) + \frac{{T_{s} }}{12}[23u_{b}^{ + } (n - 1) - 16u_{b}^{ + } (n - 2) + 5u_{b}^{ + } (n - 3)] \\ & u_{b}^{ - } (n - 1) = \frac{{\omega_{C} [U_{b} (n - 1) - \hat{U}_{b}^{ + } (n - 1) - \hat{U}_{b}^{ - } (n - 1)] - \omega_{0} [\hat{U}_{b}^{ - } (n - 1) + 2\hat{U}_{a}^{ - } (n - 1)]}}{\sqrt 3 } \\ & \hat{U}_{b}^{ - } (n) = \hat{U}_{b}^{ - } (n - 1) + \frac{{T_{s} }}{12}[23u_{b}^{ - } (n - 1) - 16u_{b}^{ - } (n - 2) + 5u_{b}^{ - } (n - 3)] \\ \end{aligned} \right.$$
(11)
$$\left\{ \begin{aligned} & u_{a} (n - 1) = \frac{{\Delta i_{a} (n - 1) - \omega_{x} [d_{a} (n - 1) + 2d_{b} (n - 1)]}}{{\sqrt 3 k_{x} }} \\& d_{a} (n) = d_{a}^{{}} (n - 1) + \frac{{k_{x} T_{s} }}{12}[23u_{a} (n - 1) - 16u_{a} (n - 2) + 5u_{a} (n - 3)] \\& u_{b} (n - 1) = \frac{{\Delta i_{b} (n - 1) + \omega_{x} [d_{b} (n - 1) + 2d_{a} (n - 1)]}}{{\sqrt 3 k_{x} }} \\& d_{b} (n) = d_{b} (n - 1) + \frac{{k_{x} T_{s} }}{12}[23u_{b} (n - 1) - 16u_{b} (n - 2) + 5u_{b} (n - 3)] \\ \end{aligned} \right.$$
(12)

Fig. 6 shows the proposed control structure of three- phase grid-connected inverter. Firstly, the grid voltages are sampled via Hall sensors. With the method in Fig. 3b, the fundamental positive sequence component of grid voltage can be obtained. And the current reference is available with (2). (Secondly, the grid current is sampled, then minus the current reference.) The current error passes the controller in (8) to get the modulation signal. Finally, the symmetrical PWM (SYPWM) [21] is used to generate the switching signals. In this way, the three-phase balanced and sinusoidal current can be achieved, which complies with IEEE Std. 929-2000.

Fig.  6
figure 6

Systematic control structure of the grid-connected inverter

Full size image

3 Experimental results

The proposed control strategy is experimentally evaluated using a three-phase grid-connected inverter. The abc-frame complex-coefficient filter and controller are digitally implemented using a 32-bit fixed-point 150 MHz TMS320F2812 DSP. The experimental parameters are as follows:the dc bus voltage is 250 V; the switching frequency is 10 kHz; L 1 = 3 mH; L 2 = 1.5 mH; and C = 9.4 uF. A resistor of 10 \(\varOmega\) is paralleled with L 2 for damping. The experimental waveform of grid voltage is shown in Fig. 7. The THDh and unbalance ratio of the grid voltage is about 5% and 30%, respectively.

Fig. 7
figure 7

Experimental waveform of grid voltage

Full size image

Fig. 8 shows experimental results in \(\omega_{x} = \omega_{0} ,\, - \omega_{0}\). The modulation signal is unbalanced to cancel the impact of unbalanced grid voltage for achieving balanced three-phase currents, as show in Fig. 8b. However, the grid current is distorted due to grid voltage harmonics. From FFT analysis in Fig. 8c, it can be observed that the dominant harmonics are 5th and 7th components.

Fig. 8
figure 8

Experimental results with \(\omega_{x} = \omega_{0} ,\; - \omega_{0}\)

Full size image

Fig. 9 shows the experimental results in case of \(\omega_{x} = \omega_{0} , - \omega_{0} , - \omega_{5} ,\omega_{7}\). In contrast with the experimental results in Fig. 8, the 5th and 7th current harmonics are eliminated. Therefore, as shown in Fig. 9b, both balanced and sinusoidal three-phase currents are achieved, which verifies the effectiveness of the proposed strategy.

Fig. 9
figure 9

Experimental results with \(\omega_{x} = \omega_{0} ,\; - \omega_{0} ,\, - \omega_{5} ,\,\omega_{7}\)

Full size image

4 Conclusion

This paper has presented a new control strategy for three-phase grid-connected inverter. The theoretical analysis and experimental results reveal that the current harmonics can be reduced and current quality is improved with the proposed solution. Also, the proposed strategy is simple and easy to implement without any frame transformation. Therefore, it is attractive for the current quality improvement of three-phase grid connected inverter in distributed generation systems.